Bir daire nasıl bölünür?

Daireyi eşit sayıda parçaya bölün -bu boş bir meslek değil, sadece hayatınızı zorlaştırmak ve bir yığın bilgi ile mutsuz bir baş düşürmek için gereklidir. Pratik bir bakış açısıyla, bu, düzenli çokgenler, pasta grafikleri, yıldız çizimi için yararlıdır. Ve sadece doğum günü pastasını paylaşabilirsin (şaka).
Nasıl bölünecek sorusu görünüyorbir bölüm üzerinde bir daire, bunun cevabı kendiliğinden ortaya çıkar: "Bir duyarlı kişinin yardımıyla". Fakat bunu, matematiksel hesaplamalara başvurmadan, ancak pusula, cetvel ve kurşun kalem kullanarak çok doğru bir şekilde yapmanın yolları vardır. Öncelikle, konstrüksiyonlarımızda merkez hatları gibi bir kavramı kullanacağımıza katılıyorum. Bunlar, 90 derecelik bir açıda R yarıçaplı (O noktası) bir çemberin merkezinde kesişen çizgilerdir. Ve bu çizgilerin daire ile kesiştiği noktalar saat yönünde 1, 2, 3 ve 4 olarak numaralandırılmıştır. Dolayısıyla davalar arasında daireyi 4 parçaya nasıl böleceğimiz sorusuna cevap verdik.
Şimdi çemberin 3'le bölünmesini öğrenineşit parçalar. İlk olarak arzu edilen nokta şimdi çevresi iki çentiği yapmak bölünebilir pusula çember yarıçapına düzeltmek ve ucunun 3 içine koyarak noktası 1'dir. Bu yüzden, birlikte noktası 1 ile iki sayı, bulmak ve üç parça halinde daire bölünme sorun çözüm olacaktır. Şimdi, aynı ilkeyi kullanarak, daireyi 12 parçaya bölebilirsiniz. 1., 2., 3. ve 12. parçaya 4 bölmek de birlikte daire çentikler ile noktalarının her biri, kavşağın, 1, 2, 3 ve 4. Elde edilen sekiz puan pusula iğne yerleştirerek seri R yarıçaplı bir daire üzerinde iki çentik ile bunun için .
Bir daireyi nasıl bölüştürme problemini çözmek için 5parçalardan önce, bir parçayı pusulayla yarısına nasıl böleceğinizi anlamanız gerekir. Bunu yapmak için, bölünebilen bölümün uzunluğunu pusulaya sabitledik ve merkezleri uç kısmına gelecek şekilde iki daire çizelim. Sonra bu dairelerin bir çizgiyi kestiği iki nokta bağlarız. Bu düz çizgi, segmentimizi yarıya böler.
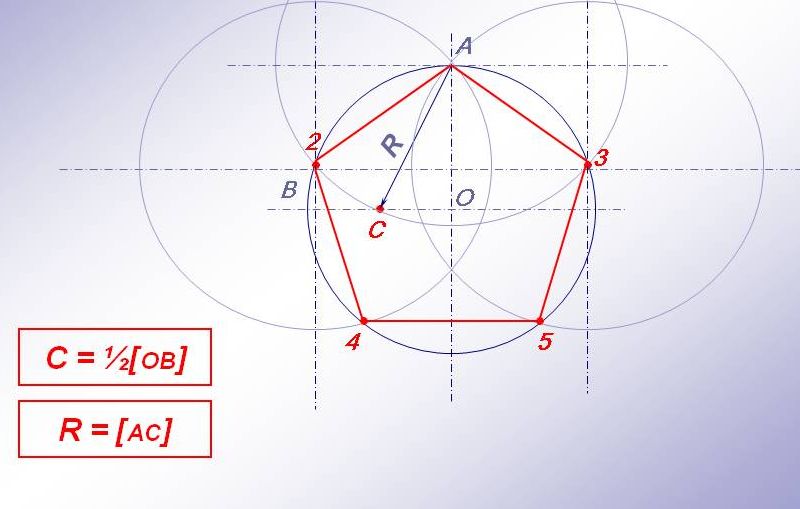
Şimdi, bu bilgiyle donanmış halde,daireyi 5 eşit parçaya bölme problemi. Parçayı daire O'nun merkezi ile nokta 4 arasında yarıya bölüyoruz. Bir E noktası elde ediyoruz. Şimdi, E1 yarıçapına göre O2 kesimi üzerinde bir çentik oluşturuyoruz. Kesişimin O2 kesimiyle kesiştiği nokta F olarak adlandırılır. Kesit EF, beşgen kenarının daireye yazılmış uzunluğudur ve sonuç olarak da köşeleri dairemizi 5 parçaya böler. Çember üzerindeki herhangi bir noktadan bir tanesini, çemberle olan kesişim noktasını tanımlayan EF yarıçapı bir yay oluşturuyoruz. Müteakip yapım, yeni inşa edilen her bir noktadan art arda gerçekleştirilir. Yapının yüksek bir doğruluğu ile son nokta başlangıçtaki ile aynı olur. Ortaya çıkan noktalar dairesini 5 eşit parçaya bölecektir.