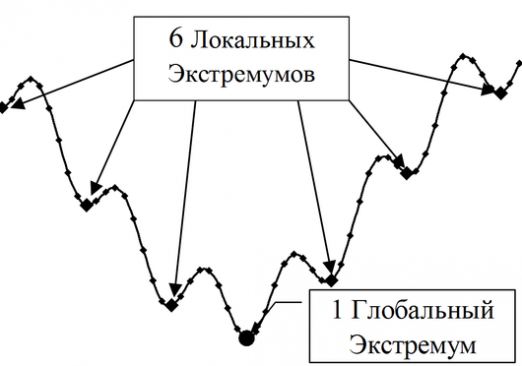
Ekstremum nasıl bulunur?

Aşırılıkları nasıl bulacağınızı öğrenmeden öncefonksiyonu için, bir ekstremumun ne olduğunu anlamak gerekir. Bir ekstremumun en yaygın tanımı, bir sayısal çizginin veya grafiğin belirli bir kümesindeki matematikteki bir işlevin en küçük veya en büyük değeri olmasıdır. Minimumun bulunduğu yerde minimumun bir ekstremumu vardır ve maksimumun maksimumun ekstremum olduğu yerde bulunur. Ayrıca, matematiksel analiz gibi bir disiplinde, yerel fonksiyonların üst sınırları seçilir. Şimdi aşırılıkları nasıl bulacağımıza göz atalım.

Matematiğin aşırıları en önemlifonksiyonun özellikleri, en büyük ve en küçük değerini gösterirler. Ekstremumlar esasen bulunan işlevlerin kritik noktalarında bulunur. İşlevin önemli ölçüde yön değiştirdiğinin ekstremum noktasında olduğunu belirtmek gerekir. Eğer ekstremum noktasının türevini hesaplarsak, o zaman tanımı gereği sıfır olmalı ya da tamamen yok olmalıdır. Bu nedenle, bir işlevin ekstremumunun nasıl bulunacağını öğrenmek için, birbirini izleyen iki görev gerçekleştirmek gerekir:

• iş tarafından tanımlanacak işlevin türevini bulmak;
• denklemin köklerini bulmak.

Ekstremumun bulunma sırası

1. Verilen f (x) fonksiyonunu yazılı olarak yazın. İlk derece f "(x) türevini bulun. Elde edilen ifade sıfıra eşittir.
2. Şimdi olan denklemi çözmek zorundasın. Ortaya çıkan çözümler u, denklemin kökleri ve belirlenen fonksiyonun kritik noktaları olacaktır.
3. Şimdi hangi kritikNoktalar (maksimum veya minimum) bulunan köklerdir. Sonraki adım, bir fonksiyonun ekstremum noktalarını bulmayı öğrendikten sonra, istenen fonksiyonun ikinci türevini bulmaktır f (x). Belirli bir eşitsizlikte bulunan kritik noktaların değerlerini ikame etmek ve sonra ne olacağını hesaplamak gerekecektir. Böyle bir durumda, ikinci türevin kritik noktada sıfırdan büyük olduğu durumda, minimum türev, minimum nokta olacak ve yoksa maksimum nokta olacaktır.
4. İlk fonksiyonun değerini hesaplamak için kalır.fonksiyonun maksimum ve minimum noktaları. Bunu yapmak için, elde edilen değerleri fonksiyonun yerine koyun ve hesaplayın. Bununla birlikte, kritik nokta maksimum ise, ekstremum maksimum olacak ve minimum ise, analojiyle minimal olacaktır.

Ekstremumun bulunması için algoritma

Kazanılan bilgiyi genellemek için ekstremum noktalarının nasıl bulunacağı ile ilgili kısa bir algoritma derleyeceğiz.

1. Belirli bir fonksiyonun tanımı alanını ve fonksiyonun kesintisiz aralıklarla tam olarak belirlediği aralıklarını buluyoruz.
2. F (x) fonksiyonunun türevini buluruz.
3. Y = f (x) denkleminin kritik noktalarını hesaplarız.
4. İşlev yönünde f (x) yönündeki değişiklikleri ve kritik noktaların fonksiyonun alanını paylaştığı türev f (x) işaretini analiz ederiz.
5. Şimdi, grafiğin her bir noktasının bir maksimum veya minimum olup olmadığını belirliyoruz.
6. İşlevin değerlerini, aşırılık olan noktalarda buluyoruz.
7. Bu çalışmanın sonucunu düzelttik -aşırılıklar ve monotonluk aralıkları. Hepsi bu kadar. Şimdi, herhangi bir aralıkta bir ekstremumun nasıl bulunabileceğini düşünmüştük. Bir işlevin belirli bir aralıkta bir ekstremum bulmanız gerekiyorsa, bu benzer bir şekilde yapılır, ancak araştırmanın sadece sınırları mutlaka dikkate alınır.

Yani, ekstremum noktalarını nasıl bulacağımızı düşünmüştükişlevi. Basit hesaplamalar yardımıyla ve türev bulguları hakkında bilgi sahibi olmakla beraber herhangi bir ekstremum bulabilir ve hesaplayabilir ve grafik olarak belirleyebilir. Ekstremum bulma, matematikte hem okulda hem de yüksek öğrenimde en önemli bölümlerden birisidir, bu nedenle onları doğru bir şekilde tanımlamayı öğrenirseniz, eğitim daha kolay ve ilginç hale gelecektir.