Bir elmasın yüksekliğini nasıl bulabilirim?
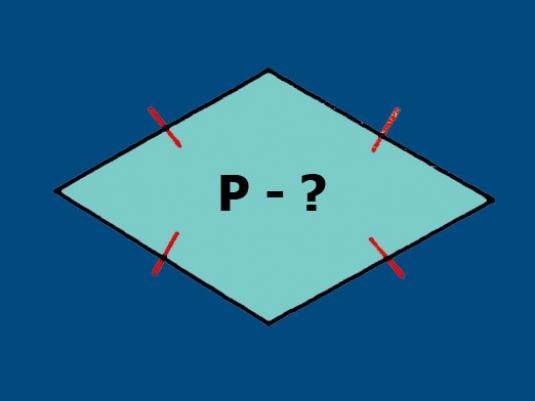
Bir eşkenar dörtgen olup, her şeyKenarlar eşittir ve karşı taraflar paraleldir. Bu durum, yüksekliği belirlemek için formülleri basitleştirir - dikey, köşeden bir kenara düşer. Her bir köşeden bir dörtgen halinde, iki tarafın yüksekliklerini düşürebilirsiniz. Eşkenar dörtgenin yüksekliğini nasıl bulacaklarını, birbirleriyle nasıl bağlantı kurduklarını düşünün.
Bir elmasın yüksekliğini nasıl bulabilirim?
Dörtgenler bu şekillerdir, bunun içinAçılar, yanların sabit uzunluklarına göre değişebilir. Bu nedenle, bir üçgenden farklı olarak, bir dörtlü kenarın uzunluklarını bilmek yetmez, açıların veya yüksekliklerin boyutlarını da belirtmek gerekir. Örneğin, elmaslar 90 ° ise, bir kare elde edilir. Bu durumda, yükseklik yanla aynı olur. Düz çizgilerin dışındaki açılarda elmasın yüksekliğini nasıl bulacağınızı düşünün.
Bir köşeden düşen elmasın iki yüksekliğinin değerini belirledik
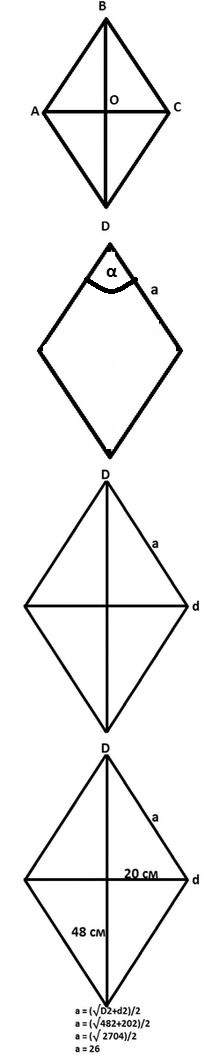
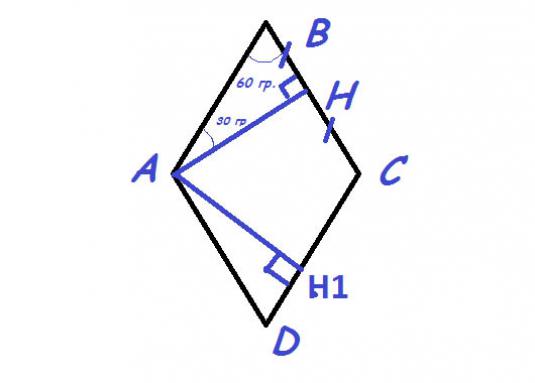
Elmas bir ABCD var, bunun için AB // CD, BC // AD, AB =BC = CD = DA = a. Yükseklik h köşeden karşı tarafa düşen dikeydir. AH yüksekliğini BC tarafına indiririz ve diğer yükseklik AN1 aynı açıdan yan DC'ye düşürülür.
- Sonra yükseklik AN = AB × sinaptB;
- Yükseklik AH1 = AD × sin dönüşümüD.
Eşkenar dörtlüğün özelliklerinden biri de karşıtlığın eşitliğidir.açılar, i. ∟B = ஆD. AB = AD (eşkenar dörtgen tüm yanları birbirine eşittir) olduğundan, AH = AH1 yüksekliği. Benzer şekilde, herhangi bir açıdan çıkarılan iki yüksekliğin birbirine eşit olduğu gösterilebilir.
Eşkenar dörtgenin diğer çapları birbirleriyle nasıl ilişkilidir?
Karşı taraflar paraleldiklerinden, bir tarafa bitişik açıların toplamı 180 ° 'dir. Sonuç olarak dört açının tümü birbirine eşittir:
- sinaklamaD = sin (180 ° - ↗D) = sinaklamaC = sinaklamaA = sinaklamaB.
Sonuç olarak, tüm yükseklikler,, birbirine eşittir ve yan, açı ve yükseklik katı bir ilişki ile birbirine bağlıdır: h = a × sinenekA, burada a herhangi bir tarafın uzunluğudur ve ⓐA eşkenar dörtgeninin herhangi bir açısıdır.