Bir dikdörtgenin genişliğini nasıl bulabilirim?

Dörtlü aralıklarla problem çözmek,Okul çocuklarına birçok zorluk getiren geometrinin en geniş kesitleri. Bir dikdörtgenin genişliğini bulmak istediğiniz tipik görevleri ele almanızı öneririz.

Her şeyden önce, ne türşekil ve temel özellikleri nelerdir. Bir dikdörtgen, tüm açıları düz, karşı tarafları eşit dörtgen biçimindedir. Yatay tarafa dikdörtgen genişliği, dikey yönde uzunluk denir.

Sorun 1. Çevrenin bilincinde genişliği hesaplayın

Bu görevi, aşağıdaki görev örneğinde analiz edelim. Dikdörtgen, çevre

36 cm, uzunluğu 16 cm'dir. Genişliği bulmak gerekiyor. Çevre, şeklin yanlarının toplamıdır. Dikdörtgenin karşıt kenarları eşit olduğu için, çevresinin formülü şu şekildedir: P = 2 (a + b), burada a ve b dikdörtgenin kenarlarıdır.

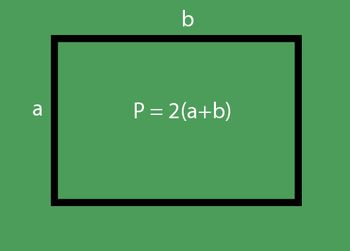
Alıyoruz:

• b = P: 2-a = 36: 2-16 = 2 (cm)

Cevap: dikdörtgenin genişliği 2 cm'dir.

Sorun 2. Uzunluğu ve çevresini bilen genişliği bulun

Görevi biraz karmaşıklaştıralım. Şimdi dikdörtgenin genişliğini, uzunluğundan 5 kat daha küçük olduğu biliniyorsa ve üçgen çevresini 120 cm bulmamız gerekir.

Sorunun koşulundan:

• a = 5b

Biliyoruz ki b = P: 2 - a. P ve a değerlerini değiştiririz. Alıyoruz:

• b = 120: 2-5b;
• 6b = 60;
• b = 60: 6
• b = 10 (cm).

Yanıt: dikdörtgenin genişliği 10 cm'dir.

Sorun 3. Alan biliniyorsa genişliğini belirleyin

Görev durumu: bahçe dikdörtgen şekle sahiptir. Alanı 400 000 m2, uzunluğu 400 m'dir. Bahçenin genişliği nedir?

Bir sebze bahçesi dikdörtgentir. Bir dikdörtgen alanı, kenarlarının çarpımına eşittir. Uzunluğu ve alanı biliyorsak genişlik eşit olacaktır:

• b = P: a = 400,000: 400 = 1000 (m)

Cevap: Bahçenin genişliği 1000 m.

Problem 4. Genişliği nasıl bulurum, diyagonal bilme

Bu görev zaten bir öncekinden biraz daha karmaşıktır. İçinde, dikdörtgenin özelliklerine ek olarak, dik açılı üçgenlerin formüllerini çağırmak gerekecektir. ABCD dikdörtgeninin AC diyagonalinin 54.6 cm ve uzunluk genişliği oranı 16: 9 olduğunu varsayalım. Figürün genişliğini bulmak gerekiyor.

Üçgen ABC'nin dik açılı olması dikdörtgen olduğu anlamına gelir. Çapraz hipotenüs, iki taraf da bacaklar.

Durumdan:

• 16AB = 9BC, dolayısıyla AB = 9BC: 16

Pisagor teoremi ile:

• AS² = AB²+ Güneş²

Rakamları yer değiştirdik:

• 54.62 = (9BC: 16)²+ Güneş²
• 2981.16 = 81BC²: 256 + Güneş²
• 2981.16 = 337BC²: 256
• 337VS² = 763176,96
• güneş² = 2264.62
• VS = 47.59 (cm)

Yanıt: üçgen genişliği 47.59 cm'dir.

Problem 5. Köşegen ve açı

ABCD'nin dikdörtgeni gösterilir, çapraz çizgisi 8 cm'dir ve açı 30 derecedir. Dikdörtgenin genişliğini bulmak gerekiyor.

Çözüm: ABC açısı düz olduğundan, üçgen ABC dikdörtgen biçimindedir,

hipotenüs, AB ve BC bacaklardır. 30 derecelik açıyla karşı karşıya kalan katet, hipotenüsün yarısına eşit olduğu bilinmektedir. Çıkıyor:

• BC = AC: 2 = 8: 2 = 4 (cm)

Cevap: dikdörtgenin genişliği 4 cm'dir.

Gördüğünüz gibi, bir dikdörtgenin genişliğini bulmak için tipik görevler oldukça basittir. Önemli olan bir dikdörtgenin formülleri ve özelliklerini ve dikdörtgen üçgenlerini bilmektir.

Bir dikdörtgenin uzunluğunu bulmak isterseniz makaleyi okuyun - Dikdörtgenin uzunluğu nedir.