Bir üçgenin çevresini nasıl bulurum?

Çoğu zaman matematiksel problemler derinanaliz, çözüm aramak ve doğru ifadeleri, formülleri seçme becerisi. Böyle bir çalışmada kafası karışık değildir. Ve yine de çözümü tek bir formülü kullanmaya indirgeyen problemler var. Bu tür sorunlar arasında bir üçgenin çevresinin nasıl bulunacağı sorusu bulunmaktadır.
Bu sorunun kararına ilişkin temel formülleri, farklı üçgenler için atıf yaparak değerlendirelim.
- Çevreyi bulmanın ana kuralıüçgen aşağıdaki ifadedir: Bir üçgenin çevresi, tüm kenarlarının uzunluklarının toplamına eşittir. P = a + b + c formülü. Burada, a, b, c üçgenin kenarlarının uzunlukları ve P çevrecidir.
- Bu formülün özel vakaları var. Örneğin:
- Sorun dikdörtgen bir üçgenin çevresini nasıl bulacağınız sorusu ise, hem klasik formülü (§ 1'e bakın) hem de daha az veri gerektiren formülü kullanabiliriz: P = a + b + √ (a2+ b2). Burada a, b sağ üçgenin bacaklarının uzunluklarıdır. Üçüncü partinin (hipotenüs) yerine Pisagor teoreminin ifadesi geldiğini görmek kolaydır.
- İkizkenar üçgeninin çevresi, P = 2 * a + b. Burada, a, üçgenin kenarının uzunluğudur ve b, tabanının uzunluğudur.
- Eşkenar (veya normal) bir üçgenin çevresini bulmak için, ifadenin değerini hesaplayın P = 3 * a, burada a üçgenin kenarının uzunluğudur.
- bu tür üçgenlerin göründüğü problemleri çözmek için, aşağıdaki ifadeyi bilmek faydalıdır: çevre oranı, benzerlik katsayısına eşittir. Formülü kullanmakta fayda var
P (ΔABC) / P (ΔA1B1C1) = k, burada ΔABC ~ ΔA1B1C1ve k benzerlik katsayısıdır.
örnek
Kenar 6, 8 ve 10 ve ΔA ile ΔABC verildiğinde1B1C1Kenar 9, 12 ile. B açısının B açısına eşit olduğu bilinmektedir1. Üçgen A'nın çevresini bulunuz1B1C1.
Çözüm
- AB = 6, BC = 8, AC = 10; bir1B1= 9; B1C1= 12. AB / A'nın1B1= BC / B1C1t. 6/9 = 8/12 = 2/3. Ve hipotez B = B ile1. Bu açılar, AB, BC ve A tarafları arasındadır.1B1, B1C1Sırasıyla. Sonuç - Üçgenlerin benzerliği için ikinci kritere göre, ΔABC ~ ΔA1B1C1. Benzerlik katsayısı k = 2/3'tür.
- Madde 1'in formülüne göre P (ΔABC) = 6 + 8 + 10 = 24 (birimler) bulalım. 2a maddesinin formülünü kullanmak mümkündür, çünkü Pisagor teoremi ΔABC'nin dikdörtgen olduğunu kanıtlıyor.
- 2d noktasından, P (ΔABC) / P (ΔA1B1C1) = 2/3. Dolayısıyla P (ΔA1B1C1) = 3 * P (ΔABC) / 2 = 3 * 24/2 = 36 (birimler).
Devamını oku:

Bir paralelkenogramın çevresini nasıl bulurum?
Elmas çevresini nasıl bulurum?

Bir poligonun çevresini nasıl bulurum?

Bir karenin çevresini nasıl bulurum?

Bir dikdörtgenin çevresini nasıl bulurum?

Çevreyi ve alanı nasıl bulacaksınız?

Bir dikdörtgenin çevresini ve alanını nasıl bulacaksınız?

Çevre nedir?
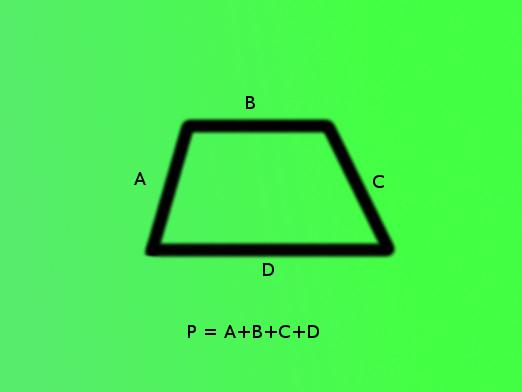
Çevreyi nasıl bulacaksınız?
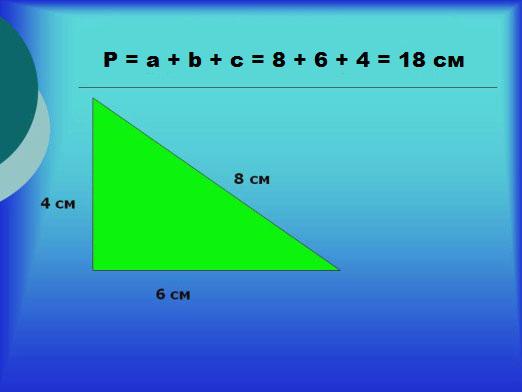
Bir üçgenin çevresi nedir?