Bir trapezoidin keskin açısının sinüsünü nasıl bulurum?

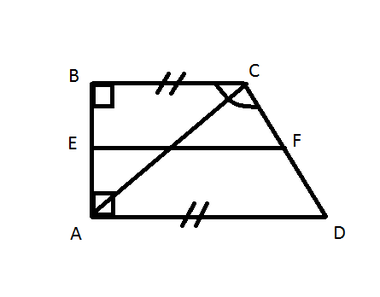
Trapez iki yanın birbirine paralel dört kenarlı olmasıdır. AD ve BC yanlarının paralel olduğu bir örnek olarak ABCD yamuk biçimini kullanarak, trapezoidin keskin açısının sinüsünün nasıl bulunacağını düşünün.
Bir izosel yamuk açısının sinüsünü arıyoruz
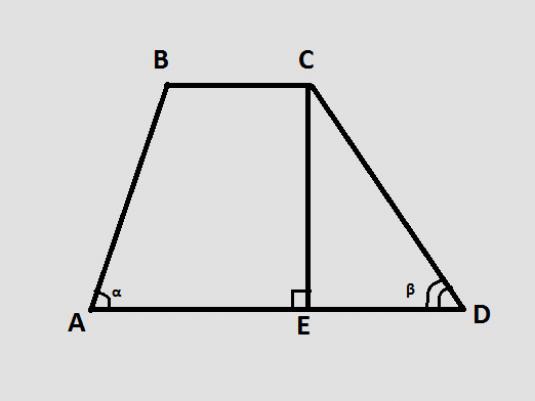
Bir iki köşeli yamuk şekli düşünelim. Bir iki köşeli trapezyumda, iki taraf eşittir. Bizim durumumuzda, AB = CD = 25 ve bazların büyüklüğü AD = 65 ve BC = 51'dir. Akut açının sinüsünü bulmaya çalışalım.
Bildiğiniz gibi, sinüs, karşıt bacağın hipotenuse oranına eşittir, bu yüzden sağ üçgene ihtiyacımız var. ABC köşesinden dikey BH'yi tabana bırakarak elde ediyoruz.
Trapezlerin önemli bir özelliği,yükseklik - genellikle taban olarak adlandırılan paralel yanlar arasındaki mesafe. Bu mesafeyi belirlemek için, dikeni, daha küçük (genellikle üst) tabanın köşesinden diğer tabana indirmeniz gerekir. Bizim durumumuzda bunlar, sinüs belirlememiz gereken VN ve CE'nin dikey çizgileri olacaktır.
Trapezoidin yüksekliğini belirleme
İki dikdörtgen üçgen alıyoruz, bacaklar BH = CE ve hipotenüs AB = CD'dir. Sonuç olarak, bu üçgenlerin diğer ayağı AH = ED'ye eşittir.
Dörtlü HBSE'de tüm açılar düzdür (HB ve CE bazlara diktir), o zaman kenarları BC = CE olan bir dikdörtgen aldık.
AD = AH + HE + ED inşaat gereğince. AH = ED ve HE = BC olduğundan, bu denklem şu şekilde yazılabilir:
- AD = 2 * AH + BC.
- AN = (AD - BC) / 2.
Sayısal değerleri değiştiririz:
- AN = (65-51) / 2 = 7.
Pisagor teoremi kullanarak, BH'nin yüksekliğini ararız:
- AV² = ВН² + АН².
- VN = √ (AV² - AN ²) = √ (25² - 7 ²) = √ (625-49) = √576 = 24
Yamuk açısının sinüsünü bulma
Şimdi VAN'ın keskin açısının sinüsünü arayın:
- sinBAH = BH / AB.
Sayısal değerleri değiştiririz:
- sinBAH = 24/25 = 0.96.
cevap:
- sinBAH = 0.96.