Sinüs nedir?

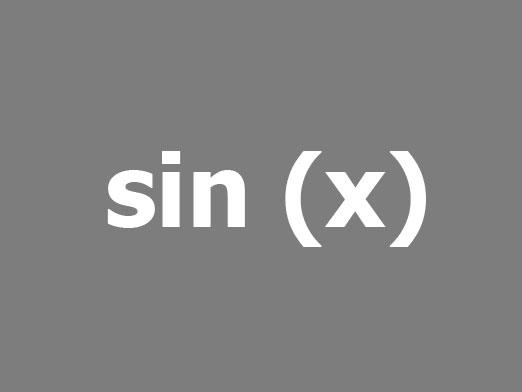
Aramızda kim onun için matematiği bağırmadıasla yararlı değil. Bütün bu abstruse formüllerin, hantal denklemlerin ve karmaşık isimlerin gerçek hayatla hiçbir ilgisi olmadığını hepimize biliyorduk. Ama er ya da geç, okulda bulduğumuz tüm bilgiler onun başvurusunu buluyor. Ve bir sinüs, kosinüs veya teğet bilerek itibarınızı kurtarabilirsiniz.

Biraz okul geometrisi

Böylece, sinüs dik açılı üçgende en-boy oranıdır. Dikdörtgen üçgenin neyin oluşturduğunu hatırlayalım.

Köşeler. Üçgendeki açıların toplamı 180^yaklaşık. İleri açısı 90'dır^yaklaşık. Dolayısıyla, toplam içindeki diğer ikisi de 90'ı^yaklaşık. Yani, bir dik açımız ve iki keskin dik açımız var.

Parti. Dikdörtgen üçgen bir hipotenüs ve iki bacaktan oluşur. İki bacak dik açı oluşturur ve hipotenüs bunun karşısında bulunur.

Bir açının sinüsu nedir? Daha önce de belirtildiği gibi, bu en-boy oranı. Ama hangileri? Akut açının sinüsü, bu açının tam karşısında yer alan bacağın hipotenöre oranıdır. Örneği düşünün:

Açı A'nın sinüsü, taraf a'nın (karşı bacak) ile yan b'ye (hipotenüs) oranıdır.

Açı C'ye ait sinüs, yan c'ye (yan taraftaki katet yatıyor) yan ilişki (hipotenüs) 'dir.

Yani, taraflar a = 3, c = 4, b = 5'e eşitse, A açısının sinüsü 3/5 olacak ve C açısının sinüsü 4/5 olacaktır.

Bunun bize ne verdiği? Şu ana kadar hiçbir şey yok, ama başka bir örneğe göz atalım. Üçgeni yanlar açarak arttıralım. Şimdi bunu yaptık:

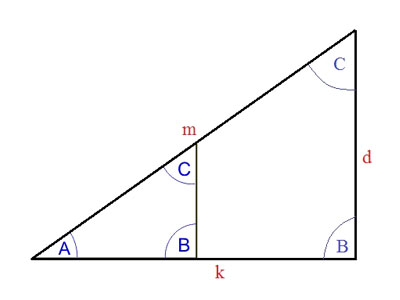
Şekilden görülebileceği gibi, tarafların uzunlukları arttı, ancak köşeler değildi. Ama en ilginç olanı - oran da değişmedi!

D = 6, k = 8, m = 10 olsun varsayalım. Ardından açı A'nın sinüsü d / m = 6/10'dur. Denklemin iki tarafıyla kesip, ilk davada olduğu gibi aynı 3/5 elde ediyoruz! Ve siz nasıl değiştiğiniz, tarafların genişletileceği veya kısaltacağı ne olursa olsun tarafların tutumu aynı kalacaktır.

Bu nedenle, sinüsün sabit bir değere sahip olduğu açıktır.

Ve şimdi - trigonometri

Antik Yunanlılar bunu uzun zamandır fark ettiler. Ana köşelerin sinüslerini hesapladılar ve bunları kaydettiler, böylece zaten hazır olan miktarları kullanmaya devam ettiler ve yenilerini icat etmediler.

Sinüsün yanı sıra açı da bir kosinüs içerir(bitişik bacağın hipotenusa bağlanması), teğet (karşı bacağın bitişikteki oranı) ve kotanjant (bitişik bacağın zıt yüzeye oranı). Bütün bu miktarlara açının trigonometrik fonksiyonları denir ve hesaplamalar ve problem çözümü için kullanılırlar.

Gizemli masalar Bradys

Her seferinde sinüs hesaplamanıza gerek yoktur. Tüm sinüsler, kosinüsler, teğetler ve kotanjantların önceden kaydedildiği, özel olarak derlenmiş Bradis tablolar vardır. Buradan bilgi alırız. Örneğin, açıyı biliyorsak, onun sinüs ve kosinüsünü biliriz. Veya tersi - eğer bir sinüs veya kosinüs biliniyorsa, hangi açı verildiğini kolayca bulabiliriz.

Doğal olarak bu trigonometrik fonksiyonlar büyüktür. Onların hepsinin imkansız olduğunu, ancak aslında gerekli olmadığını unutmayın. Esas itibariyle sadece bazılarını kullanıyorlardı.

Köşeler hakkında biraz

Fakat trigonometrik fonksiyonlar yalnızcakeskin ve dik açılardan, aptalca da olsa, fakat burada bulguları için bir daire ve koordinat eksenlerinin bir grafiğine zaten ihtiyaç duyulacaktır. Ve bu tamamen farklı bir hikaye.

sinüzoidi

Şimdi bir sinüzoidozun ne olduğunu görelim. Böyle bir sinüzoidaya benziyor:

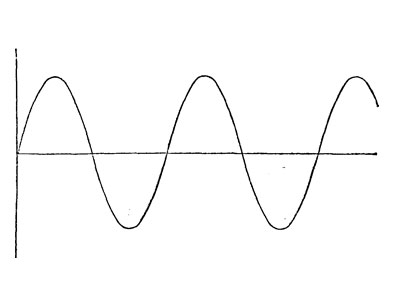
Ve sinüs değişiminin bir grafiğidir.açı değişimine bağlı olarak. Yukarıda belirtildiği gibi, taraflar değişebilir ve açı da değişmez - sinüs değişmez. Fakat açısı değişirse, en-boy oranı değişir ve dolayısıyla sinüs değeri değişir.

Sinüzoid sinüs sayısal değişiklikleri görüntüleraçısıdır ve y = sin (x) fonksiyonunun bir grafiğidir. Buradaki karmaşık hiçbir şey yok, özellikle her açıdan sinüs değerlerini Bradys tablolarında yazıyor. Fakat biz sadece en basit hatırlayacağız.

Açıların belirlenmesi hakkında biraz daha fazlası

Herkes, açıların derece cinsinden ölçülmesini veyaradyan. Bir yarıçapa benzeyen bir makas ile ölçtüğümüz dereceler. Bir derece 1/360 daire. Neden öyle? Çünkü herhangi bir açı "açılabilir" veya "kapalı" olabilir. Hatta tüm dönüş için açıp bir daire elde edebilirsiniz.

Bilindiği gibi, tam ciro, 360^yaklaşık. Düz bir çizgi 180 derecelik bir açıdır.^yaklaşık. Yani, çemberin çapı 180'dir^hakkında. Veya sayı Pi. Bu nedenle açının 90 ° olduğu söylenebilir^yaklaşık (derece cinsinden) ve Pi / 2 (radyan cinsinden).

Şimdi en temel sinüsleri hatırlamaya çalış. Aklınıza ne gelen açılar geliyor?

Doğru açı - 90^yaklaşık, Pi / 2 - sin = 1

Açılma açısı 180^yaklaşık, Pi - sin = 0

Akut açı 60^yaklaşık - Pi / 3 - sin = 0.866

Keskin açılı 45^yaklaşık - Pi / 4 - sin = 0.7071